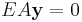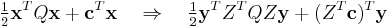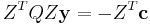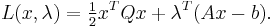Quadratic programming
Quadratic programming (QP) is a special type of mathematical optimization problem. It is the problem of optimizing (minimizing or maximizing) a quadratic function of several variables subject to linear constraints on these variables.
The quadratic programming problem can be formulated as:[1]
Assume x belongs to 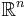 space. Both x and c are column vectors with n elements (n×1 matrices), and Q is a symmetric n×n matrix.
space. Both x and c are column vectors with n elements (n×1 matrices), and Q is a symmetric n×n matrix.
Minimize (with respect to x)
Subject to one or more constraints of the form:
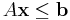 (inequality constraint)
(inequality constraint)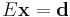 (equality constraint)
(equality constraint)
where 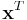 indicates the vector transpose of
indicates the vector transpose of 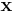 . The notation
. The notation 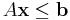 means that every entry of the vector
means that every entry of the vector 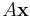 is less than or equal to the corresponding entry of the vector
is less than or equal to the corresponding entry of the vector 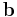 .
.
If the matrix 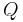 is positive semidefinite matrix, then
is positive semidefinite matrix, then  is a convex function: In this case the quadratic program has a global minimizer if there exists some feasible vector
is a convex function: In this case the quadratic program has a global minimizer if there exists some feasible vector 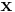 (satisfying the constraints) and if
(satisfying the constraints) and if  is bounded below on the feasible region. If the matrix
is bounded below on the feasible region. If the matrix 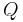 is positive definite and the problem has a feasible solution, then the global minimizer is unique.
is positive definite and the problem has a feasible solution, then the global minimizer is unique.
If 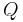 is zero, then the problem becomes a linear program.
is zero, then the problem becomes a linear program.
A related programming problem, quadratically constrained quadratic programming, can be posed by adding quadratic constraints on the variables.
Contents |
Solution methods
For general problems a variety of methods are commonly used, including
-
- interior point,
- active set[2],
- augmented Lagrangian[3],
- conjugate gradient,
- gradient projection,
- extensions of the simplex algorithm.[4]
Convex quadratic programming is a special case of the more general field of convex optimization.
Equality constraints
Quadratic programming is particularly simple when there are only equality constraints; specifically, the problem is linear. By using Lagrange multipliers and seeking the extremum of the Lagrangian, it may be readily shown that the solution to the equality constrained problem is given by the linear system:
where  is a set of Lagrange multipliers which come out of the solution alongside
is a set of Lagrange multipliers which come out of the solution alongside 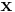 .
.
The easiest means of approaching this system is direct solution (for example, LU factorization), which for small problems is very practical. For large problems, the system poses some unusual difficulties, most notably that problem is never positive definite (even if  is), making it potentially very difficult to find a good numeric approach, and there are many approaches to choose from dependent on the problem [5].
is), making it potentially very difficult to find a good numeric approach, and there are many approaches to choose from dependent on the problem [5].
If the constraints don't couple the variables too tightly, a relatively simple attack is to change the variables so that constraints are unconditionally satisfied. For example, suppose 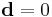 (generalizing to nonzero is straightforward). Looking at the constraint equations:
(generalizing to nonzero is straightforward). Looking at the constraint equations:
introduce a new variable 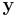 defined by
defined by
where 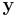 has dimension of
has dimension of 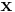 minus the number of constraints. Then
minus the number of constraints. Then
and if  is chosen so that
is chosen so that 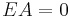 the constraint equation will be always satisfied. Finding such
the constraint equation will be always satisfied. Finding such  entails finding the null space of
entails finding the null space of  , which is more or less simple depending on the structure of
, which is more or less simple depending on the structure of  . Substituting into the quadratic form gives an unconstrained minimization problem:
. Substituting into the quadratic form gives an unconstrained minimization problem:
the solution of which is given by:
Under certain conditions on  , the reduced matrix
, the reduced matrix 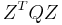 will be positive definite. It's possible to write a variation on the conjugate gradient method which avoids the explicit calculation of
will be positive definite. It's possible to write a variation on the conjugate gradient method which avoids the explicit calculation of  [6].
[6].
Lagrangian duality
The Lagrangian dual of a QP is also a QP. To see that let us focus on the case where 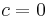 and Q is positive definite. We write the Lagrangian function as
and Q is positive definite. We write the Lagrangian function as
Defining the (Lagrangian) dual function 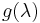 , defined as
, defined as 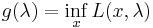 , we find an infimum of
, we find an infimum of  , using
, using 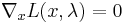 :
:
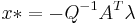 , hence the dual function is
, hence the dual function is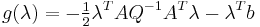
hence the Lagrangian dual of the QP is
maximize: 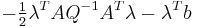
subject to: 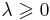 .
.
Besides the Lagrangian duality theory, there are other duality pairings (e.g. Wolfe, etc.).
Complexity
For positive definite Q, the ellipsoid method solves the problem in polynomial time.[7] If, on the other hand, Q is indefinite, then the problem is NP-hard.[8] In fact, even if Q has only one negative eigenvalue, the problem is NP-hard.[9]
Solvers and scripting (programming) languages
Free open-source permissive licenses:
| Name | License | Brief info |
|---|---|---|
| OpenOpt | BSD | Universal cross-platform numerical optimization framework, see its QP page and other problems involved. Uses NumPy arrays and SciPy sparse matrices. |
| qp-numpy | BSD | Built around the qld code written by K.Schittkowski of the University of Bayreuth, Germany |
Free open-source copyleft (reciprocal) licenses:
| Name | License | Brief info |
|---|---|---|
| CVXOPT | GPL | General purpose convex optimization solver written in Python
OOQP |
| Octave | GPL | General purpose GNU Octave solver for Quadratic Programming problems |
Other Free open-source licenses:
| Name | License | Brief info |
|---|---|---|
| CGAL | QPL | An exact solver QP_solver, part of the Computational Geometry Algorithms Library (CGAL) |
| Name | Brief info |
|---|---|
| AIMMS | |
| AMPL | |
| CPLEX | Popular solver with an API for several programming languages |
| EXCEL Solver Function | |
| FinMath | A .NET numerical library containing an interior-point primal-dual solver for convex quadratic programming problems. |
| GAMS | |
| Gurobi | Solver with parallel algorithms for large-scale linear programs, quadratic programs and mixed-integer programs. Free for academic use. |
| Lingo | |
| MATLAB | A general-purpose and matrix-oriented programming-language for numerical computing. Quadratic programming in MATLAB requires the Optimization Toolbox in addition to the base MATLAB product |
| Mathematica | A general-purpose programming-language for mathematics, including symbolic and numerical capabilities. |
| MOSEK | A solver for large scale optimization with API for several languages (C++,java,.net, Matlab and python) |
| OptimJ | Free Java-based Modeling Language for Optimization supporting multiple target solvers and available as an Eclipse plugin.[10][11] |
| Solver Foundation | A .NET platform for modeling, scheduling, and optimization |
| TOMLAB | Supports global optimization, integer programming, all types of least sqaures, linear, quadratic and unconstrained programming for MATLAB. TOMLAB supports solvers like Gurobi, CPLEX, SNOPT and KNITRO. |
| Xpress |
See also
- Support vector machine
- Sequential quadratic programming
- Quadratically constrained quadratic programming
References
Notes
- ^ Nocedal, Jorge; Wright, Stephen J. (2006). Numerical Optimization (2nd ed.). Berlin, New York: Springer-Verlag. p. 449. ISBN 978-0-387-30303-1.
- ^ Murty, K. G. (1988). Linear complementarity, linear and nonlinear programming. Sigma Series in Applied Mathematics. 3. Berlin: Heldermann Verlag. pp. xlviii+629 pp.. ISBN 3-88538-403-5. http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/. (Available for download at the website of Professor Katta G. Murty.) MR949214
- ^ F. Delbos, J.Ch. Gilbert (2005). Global linear convergence of an augmented Lagrangian algorithm for solving convex quadratic optimization problems. Journal of Convex Analysis, 12, 45-69.
- ^ Murty, K. G. (1988). Linear complementarity, linear and nonlinear programming. Sigma Series in Applied Mathematics. 3. Berlin: Heldermann Verlag. pp. xlviii+629 pp.. ISBN 3-88538-403-5. http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/. (Available for download at the website of Professor Katta G. Murty.) MR949214
- ^ Google search.
- ^ Nocedal, Jorge (2000), On the Solution of Equality Constrained Quadratic Programming Problems Arising in Optimization, SIAM Journal of Scientific Computing
- ^ Kozlov, M. K.; S. P. Tarasov and Leonid G. Khachiyan (1979). "[Polynomial solvability of convex quadratic programming]". Doklady Akademii Nauk SSSR 248: 1049–1051. Translated in: Soviet Mathematics - Doklady 20: 1108–1111.
- ^ Sahni, S. "Computationally related problems," in SIAM Journal on Computing, 3, 262--279, 1974.
- ^ Quadratic programming with one negative eigenvalue is NP-hard, Panos M. Pardalos and Stephen A. Vavasis in Journal of Global Optimization, Volume 1, Number 1, 1991, pg.15-22.
- ^ http://www.in-ter-trans.eu/resources/Zesch_Hellingrath_2010_Integrated+Production-Distribution+Planning.pdf OptimJ used in an optimization model for mixed-model assembly lines, University of Münster
- ^ http://www.aaai.org/ocs/index.php/AAAI/AAAI10/paper/viewFile/1769/2076 OptimJ used in an Approximate Subgame-Perfect Equilibrium Computation Technique for Repeated Games
Bibliography
- Cottle, Richard W.; Pang, Jong-Shi; Stone, Richard E. (1992). The linear complementarity problem. Computer Science and Scientific Computing. Boston, MA: Academic Press, Inc.. pp. xxiv+762 pp.. ISBN 0-12-192350-9. MR1150683
- Garey, Michael R.; Johnson, David S. (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A6: MP2, pg.245.
- Murty, K. G. (1988). Linear complementarity, linear and nonlinear programming. Sigma Series in Applied Mathematics. 3. Berlin: Heldermann Verlag. pp. xlviii+629 pp.. ISBN 3-88538-403-5. http://ioe.engin.umich.edu/people/fac/books/murty/linear_complementarity_webbook/. (Available for download at the website of Professor Katta G. Murty.) MR949214
External links
|
||||||||